Ch4. 모델 훈련

 

• 선형 회귀를 훈련시키는 두가지 방법
  
  • 직접 계산할 수 있는 공식 사용하여 훈련 세트에 가장 잘 맞는 모델 파라미터를 해석적으로 구하기
  • 경사 하강법 사용하여 모델 파라미터 조금씩 바꾸면서 비용 함수를 훈련 세트에 대해 최소화시키기

 

 

< 선형 회귀 >

 

• 삶의 만족도 = θ0 + θ1 * 1인당_GDP
  • 1인당_GDP에 대한 선형 함수
  • θ0, θ1 : 모델 파라미터

 

• 선형 회귀 모델의 예측 : ŷ = θ0 + θ1X1 + θ2X2 + ··· + θnXn
  • ŷ : 예측값
  • n : 특성의 수
  • Xi : i번째 특성값
  • θj : j번째 모델 파라미터

 

• 벡터 형태의 선형 회귀 모델 예측 : ŷ = h0(X) = θ · X
  • θ : 편향 θ0에서 θn까지 특성 가중치 담은 모델의 파라미터 벡터
  • X : X0에서 Xn까지 담은 샘플의 특성 벡터 ( X0은 항상 1)
  • θ · X : 벡터 θ와 X의 점곱 : θ0X0 + θ1X1 + ··· + θnXn
  • h0 : 모델 파라미터 θ를 사용한 가설함수

 

• 모델을 훈련시킨다 = 모델이 훈련 세트에 가장 잘 맞도록 모델 파라미터를 설정한다
  • 모델이 훈련 데이터에 얼마나 잘 들어맞는지 측정 필요
  • 회귀에 가장 널리 사용되는 성능 측정 지표는 평균 제곱근 오차 (RMSE)
  • 선형 회귀 모델 훈련시키려면 : RMSE를 최소화하는 θ를 찾아야 함 (실제로는 MSE를 최소화)

 

• 선형 회귀 모델의 MSE 비용 함수

 

 

 

> 정규방정식

• 비용 함수를 최소화하는 θ값을 찾기 위한 해석적인 방법

• 공식 테스트 - 선형처럼 보이는 데이터 생성

 

• 정규방정식 사용해 θ햇 값 계산
• inv() : 역행렬
• dot() : 행렬 곱셈

 

• 각각 4, 3 기대했지만 잡음 때문에 정확한 재현은 하지 못함
• θ햇 사용해 예측

 

• 모델의 예측 그래프에 나타내기

 

• 사이킷런에서 선형 회귀 수행

 

• LinearRegression 클래스는 scipy.linalg.lstsq() 함수를 기반으로
• 함수 직접 호출하기

 

• 유사역행렬 : 특잇값 분해(SVD) 사용

 

 

> 계산 복잡도

 

• 역행렬 계산하는 계산 복잡도 : O(n².⁴) ~ O(n³) : 특성 수가 두 배로 늘어나면 계산 시간이 5.3 ~ 8배 증가한다는 뜻
• 사이킷런의 LinearRegression 클래스의 SVD 방법 : O(n²) : 특성 수가 두 배로 늘어나면 계산 시간 4배

 

 

 

< 경사 하강법 >

 

• 최적화 알고리즘
• 비용 함수 최소화를 위해 반복해서 파라미터 조정
• 파라미터 벡터 θ에 대해 비용 함수의 현재 gradient 계산하고, gradient가 감소하는 방향으로 진행 (gradient가 0이 되면 최솟값)
• θ는 임의의 값으로 시작 : 무작위 초기화

 

 

 

• 중요한 파라미터 : 스텝의 크기 : 학습률 하이퍼파라미터로 결정
  • 학습률이 너무 작으면 : 시간이 오래 걸림
  • 학습률이 너무 크면 : 골짜기를 가로질러 반대편으로 건너뛰게 되어 이전보다 더 높은 곳으로 올라가게 됨
• 비용 함수는 다양한 모양
• 무작위 초기화 때문에 알고리즘이 왼쪽에서 시작하면 전역 최솟값보다 덜 좋은 지역 최솟값에 수렴
• 오른쪽에서 시작하면 평탄한 지역 지나기 위한 시간이 길고 일찍 멈추게 되어 전역 최솟값에 도달하지 못함

 

 

• 선형 회귀를 위한 MSE 비용 함수는 곡선에서 어떤 두 점을 선택해 선을 그어도 곡선을 가로지르지 않는 볼록 함수 : 지역 최솟값이 없고 하나의 전역 최솟값만. 연속된 함수이고 기울기가 갑자기 변하지 않음

 

• 모델 훈련은 훈련 세트에서 비용 함수를 최소화하는 모델 파라미터의 조합을 찾는 일

 

 

> 배치 경사 하강법

 

• 편도함수 : 각 모델 파라미터에 대한 비용 함수의 gradient 계산 = 모델 파라미터가 조금 변경될 때 비용 함수가 얼마나 바뀌는지 계산
• 파라미터 θj에 대한 비용 함수의 편도함수

 

• 다음 식을 사용하여 편도함수 한꺼번에 계산 가능

• 매 경사 하강법 스텝에서 전체 훈련 세트 X에 대해 계산
• 위로 향하는 gradient 벡터가 구해지면 반대 방향인 아래로 가야 함 : 학습률 사용

 

• 알고리즘 구현

 

• 정규방정식으로 찾은 값과 같음 : 경사 하강법 완벽 작동
• 학습률을 바꾼다면?

 

• 왼쪽 : 학습률 너무 낮음. 시간이 오래 걸릴 것
• 가운데 : 적당
• 오른쪽 : 학습률 너무 높음

 

• 적절한 학습률 찾기 : 그리드 탐색 but 수렴이 너무 오래 걸리지 않기 위해 반복 횟수 제한
• 반복 횟수 지정 : 반복 횟수 아주 크게 지정하고 gradient 벡터가 아주 작아지만 경사 하강법이 최솟값에 도달한 것이므로 알고리즘 중지

 

 

> 확률적 경사 하강법

 

• 배치 경사 하강법의 문제 : 매 스텝에서 전체 훈련 세트 이용 - 훈련 세트가 커지면 느려짐
• 확률적 경사 하강법 : 매 스탭에서 한 개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대한 gradient 계산 - 빠른 알고리즘, 큰 훈련 세트 훈련 가능 but) 확률적이므로 불안정
• 비용 함수가 불규칙할 때 알고리즘이 지역 최솟값 건너뛰도록 도와줌
• 지역 최속값에서 탈출 but 전역 최솟값에 다다르지 못함 --- 학습률을 점진적으로 감소시키기
• 매 반복에서 학습률을 결정하는 함수 : 학습 스케쥴

 

• 간단한 학습 스케쥴 사용한 확률적 경사 하강법의 구현

 

• 배치 경사 하강법 코드가 1000번 반복하는 동안 이 세트는 50번만 반복하고도 좋은 값 도달
• 각 반복 : 에포크
• 샘플을 무작위로 선택 : 어떤 샘플은 한 에포크에서 여러 번 선택되고 어떤 샘플은 전혀 선택되지 못할 수도 

 

 

> 미니배치 경사 하강법

 

• 각 스텝에서 전체 훈련 세트나 하나의 샘플을 기반으로 gradient 계산이 아니라 미니배치라 부르는 임의의 작은 샘플 세트에 대해 gradient 계산
• SGD보다 덜 불규칙하게 움직이고 최솟값에 더 가까이 도달 but 지역 최솟값에서 빠져나오기 힘들지도, 매 스텝에서 많은 시간 소요

 

• m : 훈련 샘플 수
• n : 특성 수

 

 

 

< 다항 회귀 >

 

• 비성형 데이터 학습에 선현 모델 사용
• 2차방정식으로 비선형 데이터 생성

• 직선은 이 데이터에 잘 맞지 않을 것 : 사이킷런의 PolynominalFeatures 사용
• 훈련 세트의 각 특성을 제곱하여 새로운 특성으로 추가

 

• X_poly는 이제 원래 특성 X와 이 특성의 제곱을 포함
• 확장된 훈련 데이터에 Linear Regression 적용

 

 

• 특성이 여러개일 때 다항 회귀가 특성 사이의 관계 찾을 수 있음. 

 

 

 

< 학습 곡선 >

 

• 고차 다항 회귀 적용하면 보통 선형 회귀보다 더 훈련 데이터에 잘 맞출 것

 

 

 

• 고차 다항 회귀 모델 : 훈련 데이터에 과대적합
• 선형 모델 : 과소적합
• 2차 다항 회귀 : 일반화 잘됨
• 그렇다면 --- 얼마나 복잡한 모델을 사용할지 어떻게 결정?

 

• 교차 검증
  • 훈련 데이터에서 성능 좋지만 교차 검증 점수 나쁘면 : 모델 과대적합
  • 양쪽에 모두 나쁘면 : 과소적합
• 학습 곡선
  • 훈련 세트와 검증 세트의 모델 성능을 훈련 세트 크기의 함수로 나타냄
  • 훈련 세트에서 크기가 다른 서브 세트 만들어 모델 여러번 훈련시키기
• 주어진 훈련 데이터에서 모델의 학습 곡선 그리는 함수
• 단순 선형 회귀 모델의 학습 곡선

 

 

• 훈련 데이터의 성능
  • 그래프가 0에서 시작하므로 훈련 세트에 하나 or 두개의 샘플이 있을 땐 모델이 완벽하게 작동
  • 훈련 세트에 샘플이 추가됨에 따라 비선형이기 때문에 모델이 훈련 데이터 완벽히 학습하기 불가능 (곡선이 평평해질 때까지 오차 상승)
• 검증 데이터에 대한 모델 성능
  • 모델이 적은 수의 훈련 샘플로 훈련될 때는 제대로 일반화될 수 없어서 검증 오차가 초기에 큼
  • 모델에 훈련 샘플이 추가됨에 따라 학습이 되고 검증 오차가 천천히 감소
  • but 선형 회귀 직선은 데이터를 잘 모델링할 수 없으므로 오차의 감소가 완만해져서 훈련 세트의 그래프와 가까워짐
• 같은 데이터의 10차 다항 회귀 모델의 학습 곡선

 

 

• 이전 곡선과의 차이점
  • 훈련 데이터의 오차가 선령 회귀 모델보다 낮음
  • 두 곡선 사이에 공간이 있음 -- 훈련 데이터에서의 모델 성능이 검증 데이터에서보다 나음 (과대적합 모델의 특징) but 더 큰 훈련 세트 사용하면 두 곡선 가까워짐

 

 

< 규제가 있는 선형 모델 >

 

 

> 릿지 회귀

• 규제가 추가된 선형 회귀 버전 (규제항이 비용 함수에 추가)
• 규제항 : 학습 알고리즘을 데이터에 맞추고, 모델의 가중치가 가능한 한 작게 유지되도록 노력. 훈련 동안에만 비용함수에 추가, 훈련 끝나면 모델의 성능을 규제가 없는 성능 지표로 평가
• 하이퍼파라미터 a : 모델을 얼마나 많이 규제할지 조절
  • a = 0 : 선형 회귀와 같아짐
  • a가 아주 크면 : 모든 가중치가 0에 가까워짐. 데이터의 평균 지나는 수평선 됨
• 릿지 회귀 비용 함수

 

 

 

• 선형 데이터에 몇가지 다른 a를 사용해 릿지 모델 훈련시킨 결과
  • 왼쪽 : 평범한 릿지 모델로 선형적인 예측
  • 오른쪽 : 릿지 규제 사용한 다항 회귀
  • a를 증가시킬수록 직선에 가까워짐
• 릿지 회귀의 정규방정식

• 사이킷런에서 정규방정식 사용한 릿지 회귀

 

• 확률적 경사 하강법

 

 

 

> 라쏘 회귀

• 선형 회귀의 규제된 버전
• 라쏘 회귀의 비용 함수

 

 

• 덜 중요한 특성의 가중치를 제거하려고 함 (가중치가 0)
• 자동으로 특성 선택을 하고 희소 모델을 만듦

 

 

• 서브그레이디언트 벡터

 

 

 

> 엘라스틱넷

• 릿지 회귀와 라쏘 회귀 절충
• 규제항 : 릿지와 회귀의 규제항 더하기
• 혼합 정도 : 혼합 비율 r 사용해 조절 
  • r = 0 : 릿지 회귀와 같음
  • r = 1 : 라쏘 회귀와 같음
• 엘라스틱넷 비용 함수

 

 

 

• 보통의 선형 회귀, 릿지, 라쏘, 엘라스틱넷 중 어떻게 결정?
  • 기본은 릿지
  • 쓰이는 특성이 적으면 라쏘나 엘라스틱넷
  • 특성 수가 많거나 강하게 연관되어 있다면 라쏘보다는엘라스틱

 

 

> 조기종료

• 경사 하강법과 같은 반복적인 학습 알고리즘 규제하는 방식
• 검증 에러가 최속값에 도달하면 훈련 중지

 

• 배치 경사 하강법으로 훈련시킨 복잡한 모델
• 에포크가 진행됨에 따라 알고리즘이 학습되어 훈련 세트에 대한 예측 에러와 검증 세트에 대한 예측 에러 줄어들음
• 감소하던 검증 에러가 다시 상승 : 모델이 훈련 데이터에 과대적합되기 시작
• 조기 종료 : 검증 에러가 최소에 도달하는 즉시 훈련 멈춤

 

 

< 로지스틱 회귀 >

• 샘플이 특정 클래스에 속할 확률을 추정하는 데 사용

 

 

> 확률 추정

• 입력 특성의 가중치 합 계산 후 결과를 바로 출력하지 않고 결괏값의 로지스틱을 출력

• 0과 1 사이의 값을 출력하는 시그모이드 함수

 

• 로지스틱 회귀 모델이 샘플 x가 양성 클래스에 속할 확률을 추정하면 이에 대한 예측을 쉽게 구하기 가능

 

> 훈련과 비용 함수

• 훈련의 목적 : 양성 샘플에 대해서는 높은 확률 추정하고, 음성 샘플에 대해서는 낮은 확률 추정하는 모델의 파라미터 벡터 θ 찾기
• 하나의 훈련 샘플에 대한 비용 함수

• t가 0에 가까워지면 -log(t)가 매우 커짐
  • 모델이 양성 샘플을 0에 가까운 확률로 추정하거나 음성 샘플을 1에 가까운 확률로 추정하면 비용이 크게 증가할 것
• t가 1에 가까워지면 -log(t)는 0에 가까워짐
  • 음성 샘플의 확률을 0에 가깝게 추정하거나 양성 샘플의 확률을 1에 가깝게 추정하면 비용은 0에 가까워질 것
• 전체 훈련 세트에 대한 비용 함수 : 모든 훈련 샘플의 비용을 평균한 것 (로그 손실)

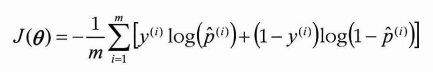
• 로지스틱 비용 함수의 편도함수

 

 

 

> 결정 경계

• 붓꽃 데이터셋 사용
• 꽃잎의 너비 기반으로 Iris-Versicolor 종 감지하는 분류기

 

• 데이터 로드

 

• 로지스틱 회귀 모델 훈련시키기

 

• 꽃잎의 너비가 0~3cm인 꽃에 대해 모델의 추정 확률 계산
  • x축 : 꽃잎 너비
  • y축 : 확률
  • 실선 : Iris virginica
  • 점선 : Not Iris virginica

 

• 양쪽의 확률이 똑같이 50%가 되는 1.6cm 근방에서 결정 경계 만들어짐
• 선형 결정 경계

 

 

• 점선 : 모델이 50% 확률을 추정하는 지점 (모델의 결정 경계)

 

 

> 소프트맥스 회귀

• 로지스틱 회귀 모델은 여러개의 이진 분류기를 훈련시켜 연결하지 않고 직접 다중 클래스를 지원하도록 일반화될 수 있음 = 소프트맥스 회귀 = 다항 로지스틱 회귀
• 샘플 x가 주어지면 소프트맥스 회귀 모델이 각 클래스 k에 대한 점수 Sk(x) 계산하고, 그 점수에 소프트맥스 함수를 적용하여 각 클래스의 확률 추정

 

• 클래스 k에 대한 소프트맥스 점수

• 샘플 x에 대해 각 클래스의 점수 계산되면 소프트맥스 함수 통과시켜 클래스 k에 속할 확률 추정 가능
• 소프트맥스 함수

 

• 로지스틱 회귀 분류기와 마찬가지로 추정 확률이 가장 높은 클래스 선택

 

• argmax 연산이 함수를 최대화하는 변수의 값 반환 (추정 확률이 최대인 k값 반환)

 

• 훈련 방법 : 크로스 엔트로피 비용 함수
  • 크로스 엔트로피 비용 함수를 최소화하는 것은 타깃 클래스에 대해 낮은 확률을 예측하는 모델을 억제
  • 추정된 클래스의 확률이 타깃 클래스에 얼마나 잘 맞는지 측정하는 용도